VorTex
0%

StyleGAN2

发表于 更新于 分类于 ，

作者针对StyleGAN遗留的问题，对模型进行了修改，进一步提高的生成图像的质量。

主要贡献

  • 修复StyleGAN存在的“水滴”的伪影。
  • 解决相位上的问题，比如侧脸上的牙齿仍然是正向。
  • 提高生成质量。

水滴伪影

水滴伪影，既出现在生成的图片上，也出现在feature map 上。虽然在生成图片上不明显，但是生成网络的很多层上都会出现（64*64以上），作者认为导致水滴的原因是因为AdaIN的风格迁移的操作， AdaIN 对每层 feature map 进行归一化，因此会潜在破坏feature map 之间的信息。

模型修改

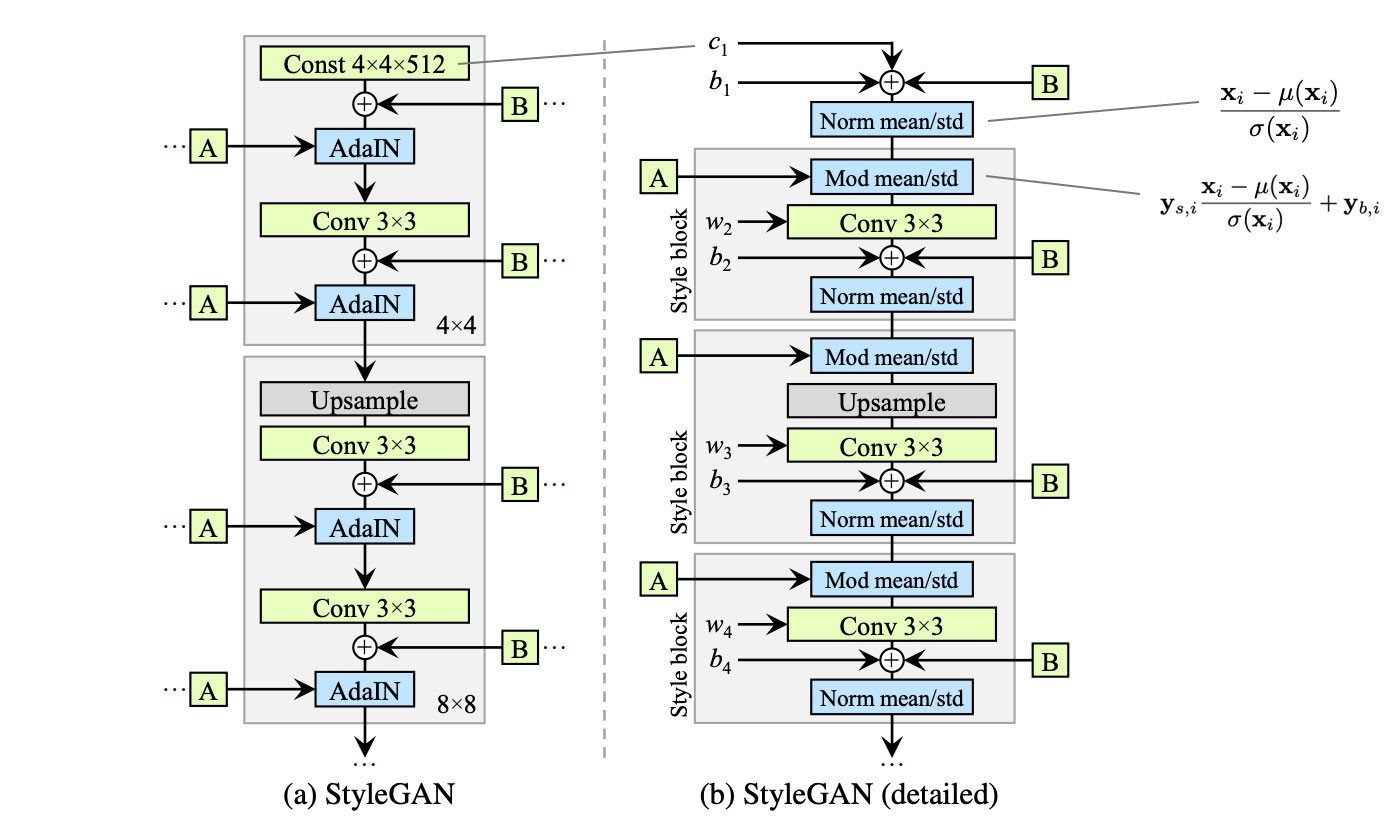
图源：https://jonathan-hui.medium.com/gan-stylegan-stylegan2-479bdf256299

从StyleGAN的结构图上可以看出，v2 做出了如下改动

  • 简化了常量c的输入方式。
  • 在规则化时去掉了取均值操作。
  • 将噪声的模块移除到style block模块之外。

weight demodulation

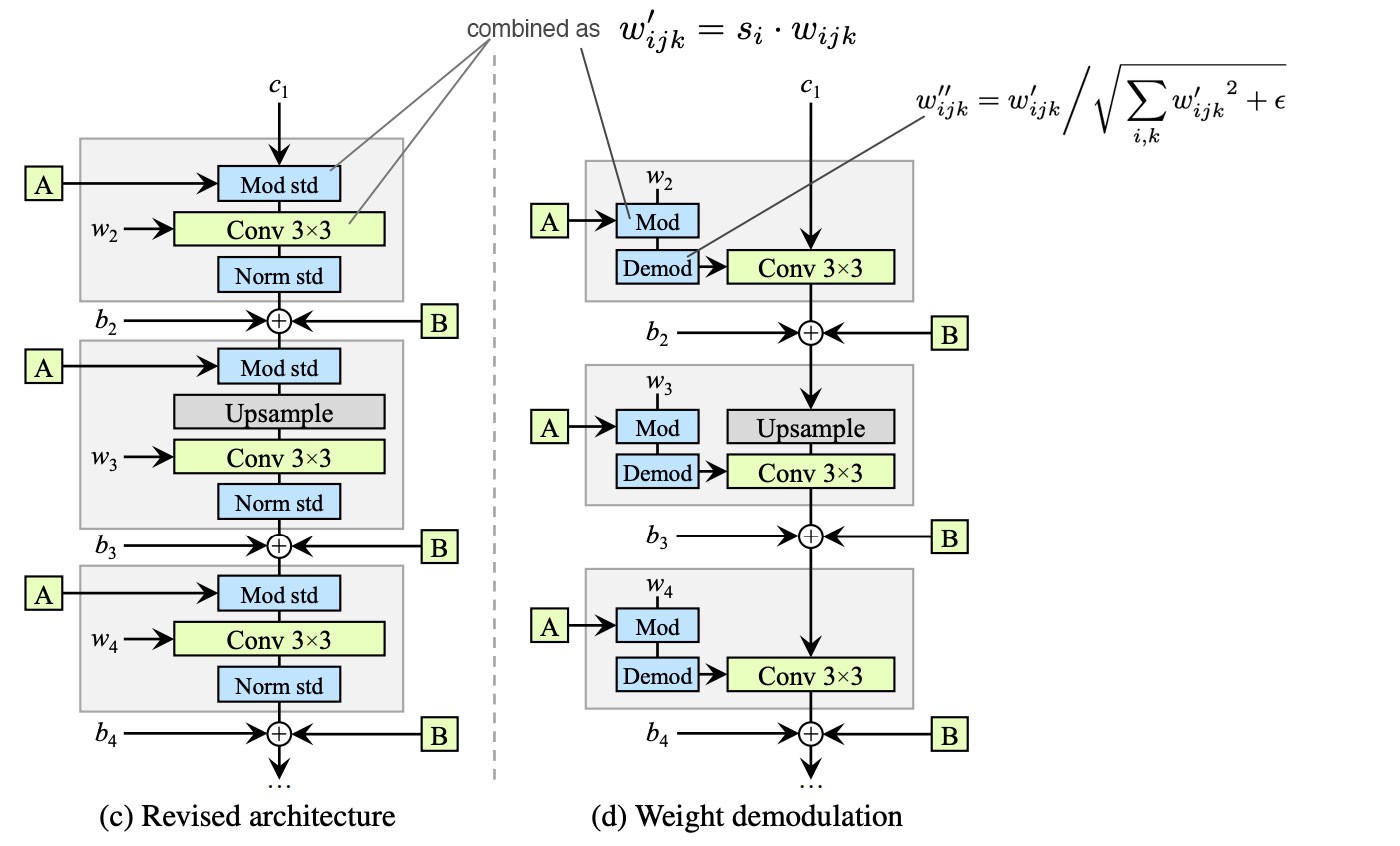
图源：https://jonathan-hui.medium.com/gan-stylegan-stylegan2-479bdf256299

\[ w^{"}_{ijk} = \frac{w^{'}_{ijk}}{\sqrt{\sum_{ij} {w^{'}_{ijk}}^{2} + \epsilon}} \]

\[ w^{'}_{ijk} = s_i \cdot w_{ijk} \]

作者将之前的缩放特征图修改为缩放卷积的权重；\(s_i\) 是第 \(i\) 个特征图的缩放比例，经过缩放之后将输出的特征图重新权重归一化。\(\epsilon\) 用来防止分母为0。 尽管从数学角度看，与实例归一化并不完全相等，但达到了近似的结果，并且训练过程更加稳定，最重要的是消除了“水滴”！

相伪问题

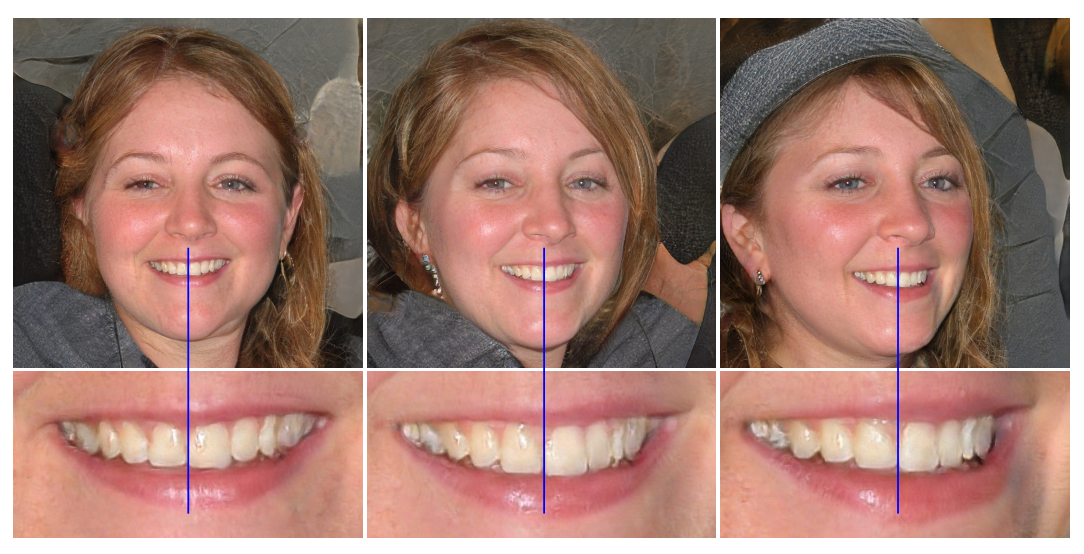
指的是生成的影响在一些高频的特征上，比如牙齿缝隙，无论怎么调整latent数值，仍然出于几个特定的位置。作者分析了特征图之后。认为这种现象和使用porgressive growing有关，所以修改了这种递进架构。选择使用残差思想的skip-connection架构。

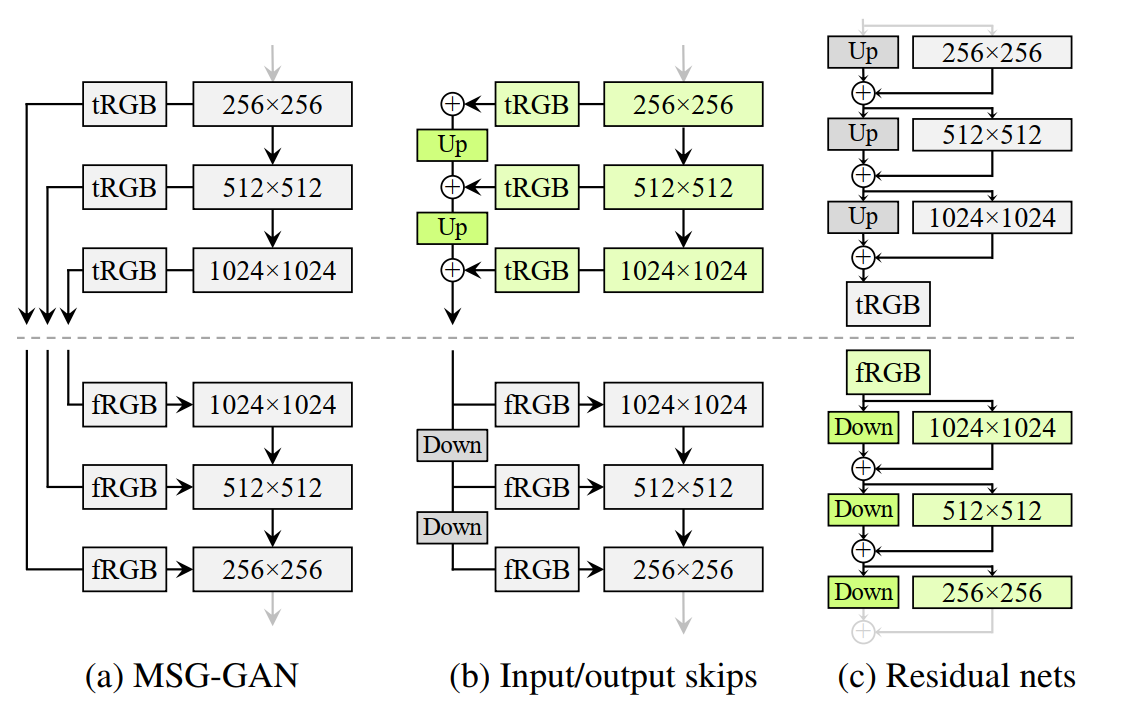
通过实验得出，生成器使用input/output skips，判别器使用Residual nets网络结构的效果最好。通过卷积和双线性上/下采样，来学习上一层和下一层之间的残差。

loss修改

延迟正则

StyleGANv1在每一次mini-batch后都会计算损失和正则，运算有些浪费，可以将一些正则简化为每隔16个batch运算一次，使得模型的性能更好了。

感知距离正则

作者提到，感知距离可以用来衡量GAN的性能，为了控制人脸的属性，我们可以改变latent code ，我们更期待在成比例改变latent code某一属性时，得到生成图片的变化也是成比例的，也就是说，当生成图片的变化和预期不同时，就会产生惩罚。

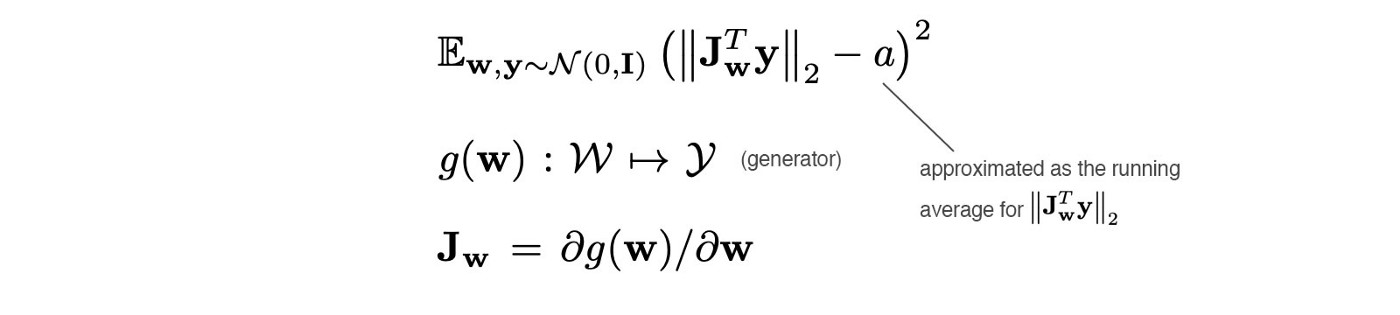\[ \mathbb{E}_{\mathbf{w},\mathbf{y} \sim \mathcal{N}\left(0, \mathbf{I}\right)} \left(||\mathbf{J}^{\mathbf{T}}_{\mathbf{w}}\mathbf{y}||_{2} - a\right)^{2} \]

\[ \mathbf{J_{w}} = \delta{g}\left(\mathbf{w}\right)/\delta{\mathbf{w}} \]

\(y\)是符合正态分布的图片，\(J_w\)是生成器\(g\)对\(w\)的一阶雅可比矩阵，表示图像在w上的变化，表示 \(\mathbf{J}^{\mathbf{T}}_{\mathbf{w}}\mathbf{y}\)的动态均值。 式中 \(\mathbf{J}^{\mathbf{T}}_{\mathbf{w}}\mathbf{y}\) 为了减少雅可比矩阵的计算量，实际由下式计算得到。 \[ \mathbf{J}^{\mathbf{T}}_{\mathbf{w}}\mathbf{y} = \nabla_{\mathbf{w}}\left(g\left(\mathbf{w}\right)·y\right) \] 通过最优化这个目标来计算这个感知距离长度正则。作者还发现更平滑的生成器可以让图片的反演更为可靠。

官方给的这部分代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# Path length regularization.
with tf.name_scope('PathReg'):

    # Evaluate the regularization term using a smaller minibatch to conserve memory.
    if pl_minibatch_shrink > 1:
        pl_minibatch = minibatch_size // pl_minibatch_shrink
        pl_latents = tf.random_normal([pl_minibatch] + G.input_shapes[0][1:])
        pl_labels = training_set.get_random_labels_tf(pl_minibatch)
        fake_images_out, fake_dlatents_out = G.get_output_for(pl_latents, pl_labels, is_training=True, return_dlatents=True)

    # Compute |J*y|.
    pl_noise = tf.random_normal(tf.shape(fake_images_out)) / np.sqrt(np.prod(G.output_shape[2:]))
    pl_grads = tf.gradients(tf.reduce_sum(fake_images_out * pl_noise), [fake_dlatents_out])[0]
    pl_lengths = tf.sqrt(tf.reduce_mean(tf.reduce_sum(tf.square(pl_grads), axis=2), axis=1))
    pl_lengths = autosummary('Loss/pl_lengths', pl_lengths)

    # Track exponential moving average of |J*y|.
    with tf.control_dependencies(None):
        pl_mean_var = tf.Variable(name='pl_mean', trainable=False, initial_value=0.0, dtype=tf.float32)
    pl_mean = pl_mean_var + pl_decay * (tf.reduce_mean(pl_lengths) - pl_mean_var)
    pl_update = tf.assign(pl_mean_var, pl_mean)

    # Calculate (|J*y|-a)^2.
    with tf.control_dependencies([pl_update]):
        pl_penalty = tf.square(pl_lengths - pl_mean)
        pl_penalty = autosummary('Loss/pl_penalty', pl_penalty)

    # Apply weight.
    #
    # Note: The division in pl_noise decreases the weight by num_pixels, and the reduce_mean
    # in pl_lengths decreases it by num_affine_layers. The effective weight then becomes:
    #
    # gamma_pl = pl_weight / num_pixels / num_affine_layers
    # = 2 / (r^2) / (log2(r) * 2 - 2)
    # = 1 / (r^2 * (log2(r) - 1))
    # = ln(2) / (r^2 * (ln(r) - ln(2))
    #
    reg = pl_penalty * pl_weight

return loss, reg