Intro
用数学的方法去变形。
Motivation
就像论文的名字一样,实现尽可能刚性的形状操纵,什么是刚性形变?刚性形变:仅包含平移和旋转的几何变换, 什么物体在刚性形变过后都保持同样的大小和形状。 所以该论文在对形状进行操纵后形变效果相比于原始的图形,尽可能保持了原始的图形的形状。
Process
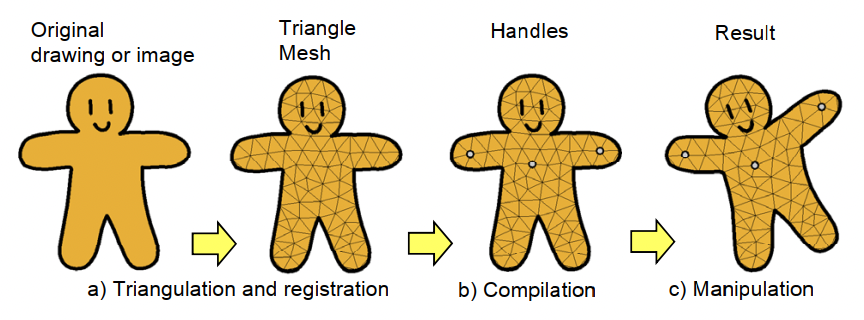
- Triangulation and registration (三角剖分 Delaunay)
- Compilation
- Manipulation
Triangulation and registration
对输入的原始图片内部利用现有很成熟的方法进行三角剖分,得到以三角面片和端点构成的集合作为输入。
Algorithm
论文的主要贡献是提出了一个两步的算法实现了形变的实时交互。第一步为每一个剖分得到的三角作出一个适当的旋转,第二步是适当的调整旋转后三角形的大小比例。核心点为定义形变前后的误差,转化为最小化能量函数优化问题。在交互开始时求解联立的方程后,我们可以在交互操作过程中快速找到自由顶点的位置。
Step One--scale-free construction
Step one generates an intermediate result by minimizing an error function that allows rotation and uniform scaling.
第一步 通过最小化一个只允许旋转和均匀缩放的误差能量函数来得到一个中间结果。均匀的缩放虽然不是刚性变换但也是一个近似刚性的变换相似变换。
算法处理的对象是三角剖分后得到的三角形,在第一步算法中可以定义三角形由其三个顶点表示\(\{v_0, v_1, v_2\}\) 。
由这三个顶点,可以定义出一个关于这个三角形的一个局部坐标系。其中设\(\overrightarrow{v_0v_1}\)为局部坐标系中的\(X\)轴正方向,\(\overrightarrow{v_0v_1}\)向量逆时针旋转\(90^{\circ}\) 定义为局部坐标系中的\(Y\)轴正方向。总体如下图所示
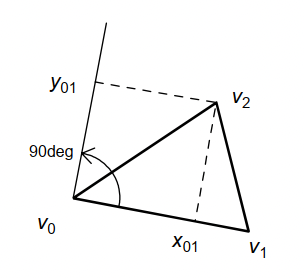
如此,就得到一个关于三角形的局部坐标系,进而可以表示在这个局部坐标系里的另一个点\(v_2\)的局部坐标\(v_2 = (x_{01},y_{01})\), 也就是说\(v_2\)可以表示为\(v_0,v_1\)的线性表达式 \[ v_2 = v_0 + x_{01}\overrightarrow{v_0v_1}+y_{01}R_{90}\overrightarrow{v_0v_1} \] 上式中\(R_{90} = \left[\matrix {0 &-1 \\ 1 & 0}\right]\),表示逆时针旋转\(90^{\circ}\)的旋转矩阵。
当图形产生形变后,图形内的每个三角形也会发生对应的形变,将形变后的三角形由新的三个点表示为\(\{v_0^\prime, v_1^\prime, v_2^\prime\}\)。由下图所示:
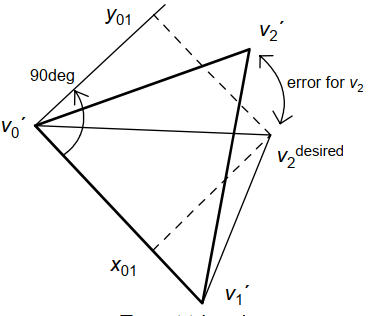
为了尽可能保持形变后三角形的形状,即在以\(\overrightarrow{v_0v_1}\)为\(X\)轴正向,\(R_{90}\overrightarrow{v_0v_1}\)为\(Y\)轴正向的坐标系下,\(v_2^\prime\)要尽可能接近原三角形的 \(v_2^{desired}\) 。即在局部坐标系下其对应位置坐标\((x_{01},y_{01})\)不变。其中由前文易知 \[ v_2^{desired} = v_0^\prime + x_{01}\overrightarrow{v_0^\prime v_1^\prime}+y_{01}R_{90}\overrightarrow{v_0^\prime v_1^\prime} \] 则 \(v_i^{desired}\) 和 \(v_i^{\prime}\)之间的误差可以表示为 \[ E_{\{v\prime\}} = ||v_i^{desired} -v_i^{\prime}|| \] 优化目标,即能量函数就是使得剖分后得到的三角形中所有顶点误差最小,尽可能使得三角形保持住最初的形状。
显然由能量函数的定义可知, \(E\)的值将其展开肯定式一个关于 \(v\prime\) 的等式
\[v\prime=(v_{0x}^{\prime}, v_{0y}^{\prime},v_{1x}^{\prime},v_{1y}^{\prime},v_{2x}^{\prime},v_{2y}^{\prime})\]
可以讲能量函数展开得到下式: \[ E_{\left\{v_{2}\right\}}=\left(v_{0 x}{ }^{\prime}+x_{01}\left(-v_{0 x}{ }^{\prime}+v_{1 x}{ }^{\prime}\right)+y_{01}\left(v_{0 y}{ }^{\prime}-v_{1 y}{ }^{\prime}\right)-v_{2 x}\right)^{2}+\left(v_{0 y}{ }^{\prime}+y_{01}\left(-v_{0 x}{ }^{\prime}+v_{1 x}{ }^{\prime}\right)+x_{01}\left(-v_{0 y}{ }^{\prime}+v_{1 y}{ }^{\prime}\right)-v_{2 y}{ }^{\prime}\right)^{2} \] 展开上式,系数矩阵 \(G\) 可以表示为 \[ \left(\begin{array}{cccccc} x_{0,1}^{2}-2 x_{0,1}+y_{0,1}^{2}+1 & 0 & -x_{0,1}^{2}+x_{0,1}-y_{0,1}^{2} & -y_{0,1} & x_{0,1}-1 & y_{0,1} \\ 0 & x_{0,1}^{2}-2 x_{0,1}+y_{0,1}^{2}+1 & y_{0,1} & -x_{0,1}^{2}+x_{0,1}-y_{0,1}^{2} & -y_{0,1} & x_{0,1}-1 \\ -x_{0,1}^{2}+x_{0,1}-y_{0,1}^{2} & y_{0,1} & x_{0,1}^{2}+y_{0,1}^{2} & 0 & -x_{0,1} & -y_{0,1} \\ -y_{0,1} & -x_{0,1}^{2}+x_{0,1}-y_{0,1}^{2} & 0 & x_{0,1}^{2}+y_{0,1}^{2} & y_{0,1} & -x_{0,1} \\ x_{0,1}-1 & -y_{0,1} & -x_{0,1} & y_{0,1} & 1 & 0 \\ y_{0,1} & x_{0,1}-1 & -y_{0,1} & -x_{0,1} & 0 & 1 \end{array}\right) \]
本算法以三角形为单位,三角形的每个顶点都要计算一次误差函数,每个三角形有 \(E = E_{v_1^\prime} + E_{v_2^\prime} + E_{v_0^\prime}\), 所以有 \(E = \sum^n_{i=0}||v_i^{disired} - v_i ^\prime||^2\) 。每个点是存在于不同的三角形里的,误差是累加计算的。 其中所有的点 \(v^\prime\) 可以被分为自由点 \(u\) 和控制点 \(q\) , 将所有点和按先 \(u\) 后 \(q\) 的顺序排列,可以构造系数矩阵 \(G= \left[\matrix {G_{00} &G_{01} \\ G_{10} & G_{11}}\right]\)。 能量函数可以表示为二次式形式。 \[ E_{1}=\mathbf{v}^{\prime \mathbf{T}} \mathbf{G} \mathbf{v}^{\prime}=\left(\begin{array}{l} \mathbf{u} \\ \mathbf{q} \end{array}\right)^{\mathrm{T}}\left[\begin{array}{ll} \mathbf{G}_{00} & \mathbf{G}_{01} \\ \mathbf{G}_{10} & \mathbf{G}_{11} \end{array}\right]\left(\begin{array}{l} \mathbf{u} \\ \mathbf{q} \end{array}\right) \] 对自由点 \(u\) 求偏导,使得偏导数为0, 来构造最小化误差得下式 \[ \frac{\partial E_{1}}{\partial \mathbf{u}}=\left(\mathbf{G}_{00}+\mathbf{G}_{00}^{\mathrm{T}}\right) \mathbf{u}+\left(\mathbf{G}_{01}+\mathbf{G}_{10}^{\mathrm{T}}\right) \mathbf{q}=\mathbf{0} \] 令 \(G^\prime = \left(\mathbf{G}_{00}+\mathbf{G}_{00}^{\mathrm{T}}\right)\) , \(B = \left(\mathbf{G}_{01}+\mathbf{G}_{10}^{\mathrm{T}}\right)\) 将上式表示为 \(G^\prime u + Bq = 0\) , 式中\(G^\prime\)和\(B\)都是固定的矩阵。矩阵元素都是由类似于局部坐标 \((x_{01}, y_{01})\) 的组合成的,而这些局部坐标都是来自于输入的原始图形中的那些三角形,所以\(G^\prime\)和\(B\) 可以在程序输入图形后做一次预计算 即可。另外控制点 \(q\) 是随用户的拖动而实时变化的,\(q\) 的坐标我们可以实时获取。
在读取完三角形,做了预计算后,只剩下自由点 \(u\) 为未知量, 只需要 对\(u\) 求导,求解方程,解出未知数。计算量小,可以在实时完成
Step Two --scale adjustment
第二步以第一步的结果当作第二步输入来调整网格中的三角形的比例,第二大步算法中可以划分为两小步:
2.1 step
将每个三角形的原始三角形的三个点通过"旋转+平移,不包括裁剪和缩放" 来拟合到第一步生成的对应三角形。
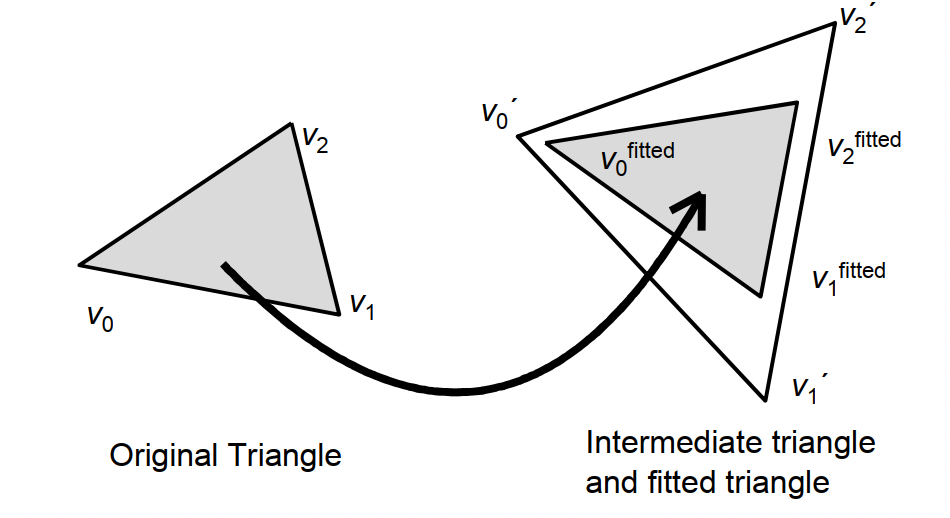
如图所示, \(v^\prime\) 表示算法中第一步时生成的三角形。 我们要使原始的三角形的三个顶点在通过“旋转+平移”时最小化原始三角形和第一步生成的三角形对应点的误差和。 \[ E_{\mathrm{f}\left\{v_{0}^{fitted}, v_{1}^{fitled}, v_{2}^{fited }\right\}}=\sum_{i=1,2,3}\left\|v_{i}^{fitted}-v_{i}{ }^{\prime}\right\|^{2} \] 其中像第一步一样 \(v_{2}^{\text {fitted }}=v_{0}^{\text {fitted }}+x_{01} \overrightarrow{v_{0}^{\text {fitted }} v_{1}^{\text {fitted }}}+y_{01} R_{90} \overrightarrow{v_{0}^{\text {fitted }} v_{1}^{\text {fitted }}}\)
在这一小步,我们针对的依然是三角形。但是在对三角形变形时,每个三角形单独最小化误差和,在这一小步,三角形与三角形之间是相互独立的。对于每个三角形,定义\(w=\left(v_{0 x}^{\text {fitted }}, v_{0 y}^{\text {fitted }}, v_{1 x}^{\text {fitted }}, v_{1 y}^{\text {fitted }}\right)^{T}\), 为了最小话能量函数\(E_f\), 像第一步一样写成系数矩阵的形式$ E_{f}=w^{T} F w $ ,对\(w\) 求偏导得 \[ \frac{\partial E_{f}}{\partial w}=\left(F+F^{T}\right) w+C=0 \] 求解一个\(4 \times 4\) 线性方程,\(F\)是一个固定的矩阵,\(C\) 可以通过第一步的结果计算得到。通过此可以得到一个和原始三角形相似的新的的三角形\(\left\{v_{0}^{fitted}, v_{1}^{fitled}, v_{2}^{fited }\right\}\), 通过按比例缩放\(\left\|v_{0}^{\text {fitted }}-v_{1}^{\text {fitted }}\right\| /\left\|v_{0}-v_{1}\right\|\),使三角形变得全等。
2.2 step
第一小步的目的是将原始三角形“旋转”和“平移”到一个第一步算法得到的三角形对应 “点与点距离和最小” 某个位置。而第二小步的目的是将三角形对应的“边与边”之间优化。
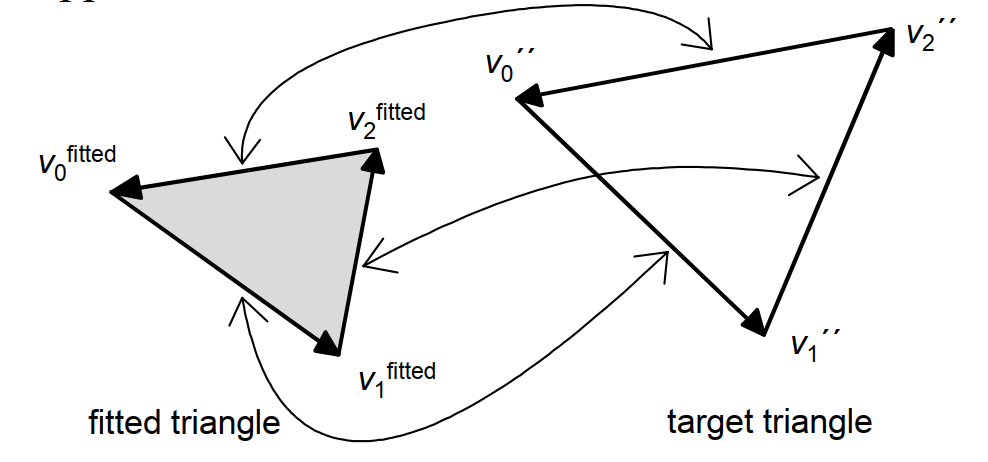
和之前一样可以将误差函数三条边的误差和表示为,注意现在计算的是边的误差和,和之前计算点的误差和不一样。 \[ E_{2\left\{v_{0}{ }^{\prime \prime} v_{1}{ }^{\prime \prime}, v_{2}{ }^{\prime \prime}\right\}}=\sum_{(i, j) \in\{(0,1),(1,2),(2,0)\}}\left\|\overrightarrow{v_{i}{ }^{\prime \prime} v_{j}{ }^{\prime \prime}}-\overrightarrow{v_{i}{ }^{\text {fitted }} v_{j}{ }^{\text {fitted }}}\right\|^{2} \] 和第一步时一样,把所有的点按照自由点\(u\)和控制点\(q\)点重排,重写误差函数。 \[ E_{2}=v^{\prime \prime T} H v^{\prime \prime}+f v^{\prime \prime}+c=\left(\begin{array}{l}u \\ q\end{array}\right)^{T}\left[\begin{array}{cc}H_{00} & H_{01} \\ H_{10} & H_{11}\end{array}\right]\left(\begin{array}{l}u \\ q\end{array}\right)+\left(\begin{array}{ll}f_{0} & f_{1}\end{array}\right)\left(\begin{array}{l}u \\ q\end{array}\right)+c \] 和前面的步骤一样求偏导数
\[ \frac{\partial E_{2}}{\partial \mathbf{u}}=\left(\mathbf{H}_{00}+\mathbf{H}_{00}^{\mathrm{T}}\right) \mathbf{u}+\left(\mathbf{H}_{01}+\mathbf{H}_{10}^{\mathrm{T}}\right) \mathbf{q}+\mathbf{f}_{0}=\mathbf{0} \]
\[ \mathbf{H}^{\prime} \mathbf{u}+\mathbf{D q}+\mathbf{f}_{0}=\mathbf{0} \]
显然,矩阵 \(H^\prime\) 和矩阵 \(D\) 都是系数矩阵 \(H\) 的子矩阵构成的,\(f_0\) 就是系数向量\(f\), 在推导能量方程时仅针对了一条边,但实际在计算中需要遍历三角形中的三个边。
通过计算可以得到 \[ H=\left(\begin{array}{cccc} 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1 \\ -1 & 0 & 1 & 0 \\ 0 & -1 & 0 & 1 \end{array}\right) \]
\[ f=\left\{-2 v_{0, x}^{f}+2 v_{1, x}^{f},-2 v_{0, y}^{f}+2 v_{1, y}^{f}, 2 v_{0, x}^{f}-2 v_{1, x}^{f}, 2 v_{0, y}^{f}-2 v_{1, y}^{f}\right\} \]
至此,我们就可以由矩阵\(H\) 求出 \(H^\prime\) 和 \(D\)。
很显然,\(H^\prime\) 和 \(D\) 都是固定的数值组成的矩阵。系数向量由$ f $第二步算法的第一小步的结果生成。 这些矩阵都可以在选定控制点 \(q\) 后,做出预计算,然后未知的点 \(u\) 可以通过求解能量函数得到。 可以满足形变过程中实时性的需求。做到实时交互。
Appendix

Reference
- 无雨森的技术分享(wechat公众号)
- 用数学编辑3D模型
- As-Rigid-As-Possible Shape Manipulation