Implementing As-Rigid-As-Possible Shape Manipulation

Intro

作者在发表ARAP后，于2009年又发表一篇基于ARAP实现上的改进工作。使实现变得更简洁通用。其中主要有两个主要改进。

使用边为变形的基本单位。提高了代码的简洁性。
控制形变交互时，无需点击三角化后图像上的顶点，点击其中任意坐标即可。

和ARAP一样，算法的目标是在形变过程中，变换尽可能刚性，最小化每个三角形的扭曲。由于是一个非线性问题，得不到问题的解析解，所以作者将一个非线性优化问题近似分解为一系列的线性问题。第一步允许旋转和平移，以及一致缩放(uniform scaling),惩罚非一致性缩放。第二步将第一步得到的结果通过进行自由平移得到最终的结果。这时惩罚旋转，和缩放。

Algorithm

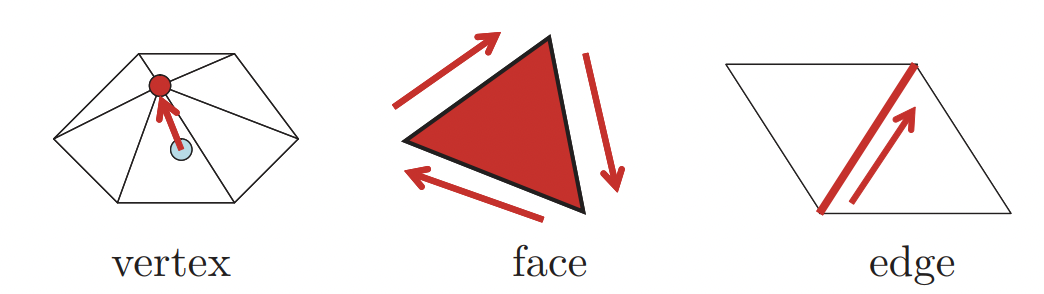
在之前的文章里，作者选择面片来表现三角形的扭曲，而在这里却选择用边来表现扭曲。对于表现扭曲变换来说，点不是个好选择。而面片相比于边来说更为直观表现刚性。所以作者在前一篇文章里选择的就是面片。但是由于使用面片相比于边来说，要计算三角形的三个边来定义扭曲。不利于编程实现。所以在这里选择基于边的实现。$v_i - v_j$。

Baseline

问题定义，为了变形后的图形尽可能接近原始图形，可以定义为下式： \[ v_{j}^{\prime}-v_{i}^{\prime}=v_{j}-v_{i}(\{i, j\} \in E) \text { subject to constraints } v_{i}^{\prime}=C_{i} \quad(i \in C) \] 其中$E$表示顶点序号为 ${i,j}$ 的边的集合，$v_j^{\prime} - v_i^{\prime}$ 表示变形后边向量， $v_j- v_i$ 表示对应的变形前的边向量， $C_i$表示变形时选择的控制点元素，$C$表示控制点的集合。根据上式可以得到一个优化方程 \[ \arg \min _{v^{\prime} \in V}\left\{\sum_{\{i, j\} \in E}\left\|\left(v_{j}{ }^{\prime}-v_{i}^{\prime}\right)-\left(v_{j}-v_{i}\right)\right\|^{2}+\sum_{i \in C}\left\|\omega\left(v_{i}{ }^{\prime}-C_{i}\right)\right\|^{2}\right\} \] $\omega$表示权重，论文里默认配置 $\omega = 1000$ , 上式优化方程中 $v_{j}-v_{i}$ 在三角面片划分好之后就是常数, $C_i$ 在选定控制点之后也是常数，变量为$v^{\prime} = (v_0^{\prime}, v_1^{\prime}, \cdots, v_n^{\prime})^T$ 。所以可以将公式抽象为下式 \[ \arg \min _{v^{\prime}}\left\|A v^{\prime}-b\right\|^{2} \] 把上式展开来表示就变成了 \[ \underbrace{\left[\begin{array}{cc} 1 & & -1 & \\ & -1 & 1 & \\ & & \vdots & \\ \hline & & w & \\ w & & & \\ & & \vdots & \\ \end{array}\right]}_{\mathrm{A}} \underbrace{\left[\begin{array}{c} v_{0 x}^{\prime} \\ v_{1 x}^{\prime} \\ \vdots \\ \\ \end{array}\right]}_{\mathbf{v}_{x}^{\prime}} -\underbrace{\left[\begin{array}{c} e_{0x} \\ e_{1x} \\ \vdots \\ \hline \omega c_{0x} \\ \omega c_{1x} \\ \vdots \end{array}\right]}_{b} \]

可以简单分析下， $\boldsymbol{v}^{\prime}=\left(\begin{array}{cc} \mathcal{v}_{0 x} & \mathcal{v}_{0 y} \\ \mathcal{v}_{1 x} & \mathcal{v}_{1 x} \\ \vdots & \vdots \\ \mathcal{v}_{n x} & \mathcal{v}_{n x} \end{array}\right)$ , 可以拆成两个矩阵$v_x^{\prime}, v_y^{\prime}$ 。则可表示$v^{\prime}=(v_x^{\prime} \quad \vdots \quad v_y^{\prime})$ 。同理可以将 $b$ 也表示为相同的形式$(b_x^{\prime} \quad \vdots \quad b_y^{\prime})$ 。把 $A v^{\prime}-b$ 可以表示为 \[ \begin{aligned} &A v^{\prime}-b \\ &\Leftrightarrow A\left(v_{x}^{\prime} \quad \vdots \quad v_{y}^{\prime}\right)-\left(b_{x} \quad \vdots \quad b_{y}\right) \\ &\Leftrightarrow\left(A v_{x}^{\prime}-b_{x} \quad \vdots \quad A v_{y}^{\prime}-b_{y}\right) \end{aligned} \] 如果对上面这个向量求模平方，可以相当于把两部分元素分别取模再求和，则有 \[ \begin{aligned} &\arg \min _{v^{\prime}}\left\|A v^{\prime}-b\right\|^{2} \\ &\Leftrightarrow \arg \min _{v^{\prime}}\left(\left\|A v_{x}{ }^{\prime}-b_{x}\right\|^{2}+\left\|A v_{y}{ }^{\prime}-b_{y}\right\|^{2}\right) \\ &\Leftrightarrow \arg \min _{v^{\prime}}\left\|A v_{x}{ }^{\prime}-b_{x}\right\|^{2}+\arg \min _{v^{\prime}}\left\|A v_{y}{ }^{\prime}-b_{y}\right\|^{2} \end{aligned} \] 此外也有 \[ \begin{aligned} &\left\{\begin{array}{l} \overrightarrow{E_{1}}=A_{1} \vec{v}+\overrightarrow{b_{1}} \\ \overrightarrow{E_{2}}=A_{2} \vec{v}+\overrightarrow{b_{2}} \end{array}\right. \\ & \\ &\vec{E}=\left[\begin{array}{l} \overrightarrow{E_{1}} \\ \cdots \\ \overrightarrow{E_{2}} \end{array}\right]=\left[\begin{array}{c} A_{1} \\ \cdots \\ A_{2} \end{array}\right] \vec{v}+\left[\begin{array}{l} \overrightarrow{b_{1}} \\ \cdots \\ \overrightarrow {b_{2}} \end{array}\right] \\ &\|\overrightarrow{E}\|^{2}=\left\|\begin{array}{l} \overrightarrow{E_{1}} \\ \cdots \\ \overrightarrow {E_{2}} \end{array}\right\|^{2}=\left\|\overrightarrow{E_{1}}\right\|^{2}+\left\|\overrightarrow{E_{2}}\right\|^{2}=\left\|A_{1} \vec{v}+\overrightarrow{b_{1}}\right\|^{2}+\left\|A_{2} \vec{v}+\overrightarrow{b_{2}}\right\|^{2} \end{aligned} \] 由于$x,y$表示形式基本相同，仅看 $x$ ，可以将能量方程表示为 \[ \arg \min _{v_{v_{i x}^{\prime}}{ }^{\prime} \mid v_{x}^{\prime}}\left\{\sum_{\{i, j\} \in E}\left\|\left(v_{j x}{ }^{\prime}-v_{i x}{ }^{\prime}\right)-\left(v_{j x}-v_{i x}\right)\right\|^{2}+\sum_{i \in C}\left\|\omega\left(v_{i x}{ }^{\prime}-C_{i x}\right)\right\|^{2}\right. \] 上式可以化为 $A v^{\prime}-b$ 的形式，其中有 \[ \underbrace{\sum_{\{i, j\} \in E}\left\|\left(v_{j x}{ }^{\prime}-v_{i x}{ }^{\prime}\right)-\left(v_{j x}-v_{i x}\right)\right\|^{2}}_{\sum_{i<=n}\left\|A_{1} v_{x}{ }^{\prime}-b_{1}\right\|^{2}} \] 和 \[ \underbrace{\sum_{i \in C}\left\|\omega\left(v_{i x}{ }^{\prime}-C_{i x}\right)\right\|^{2}}_{\sum_{k=n}\left\|\omega\left(A_{2} v_{x}{ }^{\prime}-b_{2}\right)\right\|^{2}} \] 把这两个组合起来，就能写成 \[ \sum_{i<=n}\left\|\left[\begin{array}{c} A_{1} \\ \cdots \\ \omega A_{2} \end{array}\right] v_{x}{ }^{\prime}-\left[\begin{array}{c} b_{1} \\ \cdots \\ \omega b_{2} \end{array}\right]\right\|^{2} \]

这个式子和论文里的式子(下式)是不是结构就一致了，对应的位置值的意义就明白了。 \[ \underbrace{\left[\begin{array}{cc} 1 & & -1 & \\ & -1 & 1 & \\ & & \vdots & \\ \hline & & w & \\ w & & & \\ & & \vdots & \\ \end{array}\right]}_{\mathrm{A}} \underbrace{\left[\begin{array}{c} v_{0 x}^{\prime} \\ v_{1 x}^{\prime} \\ \vdots \\ \\ \end{array}\right]}_{\mathbf{v}_{x}^{\prime}} -\underbrace{\left[\begin{array}{c} e_{0x} \\ e_{1x} \\ \vdots \\ \hline \omega c_{0x} \\ \omega c_{1x} \\ \vdots \end{array}\right]}_{b} \]

$A_1$ 中的1，-1表示对应位置的 $v_{ix}^{\prime} - v_{jx}^{\prime}$。$ e_{ix}$ 表示的就是对应的 $v_{ix} - v_{jx}$，其值在三角剖分表示完后，就是一个定值。$\omega$ 对应位置为控制点。最后对形如$||A v^{\prime}-b||^2$最小二乘优化问题。可以得到 \[ A^{T} A v^{\prime}=A^{T} b \] 通过求解这个方程就能得到变形后所有点的新坐标，$y$ 分量也是一样的操作。$v^{\prime} = (A^{T}A)^{-1}A^Tb$

Step One - 相似性变换

首先对于图中的边$e_k$进行相似变换。

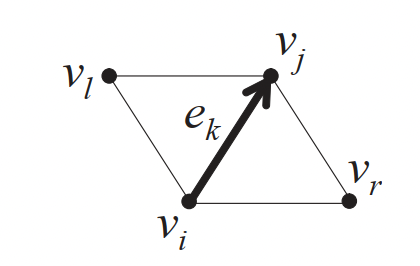
将边 $e_k$ 对应的邻接点可以表示为$N(e_k) = \{v_i, v_j, v_l, v_r\}$ $l$ 表示left， $r$ 表示right。当 $e_k$ 表示的是边界边时，则对应的邻接点只有三个。论文里对旋转定义了一个旋转变换 $T_{k}=\left[\begin{array}{cc} \mathcal{c}_{k} & s_{k} \\ -s_{k} & \mathcal{c}_{k} \end{array}\right]$ $c$ 表示 $\cos$ , $s$ 表示$\sin$. $T$ 表示Transformation。旋转变换的目的是让边 $e_k$ 的邻接点在变形时位置尽量不变。那么优化方程表示为 \[ T_{k}=\arg \min _{T_{k}} \sum_{v \in N\left(e_{k}\right)}\left\|T_{k} v-v^{\prime}\right\|^{2} \]

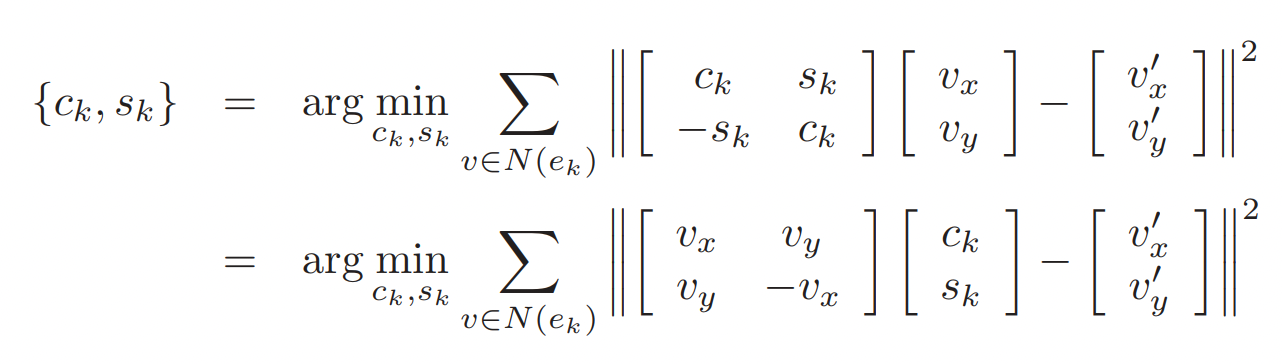
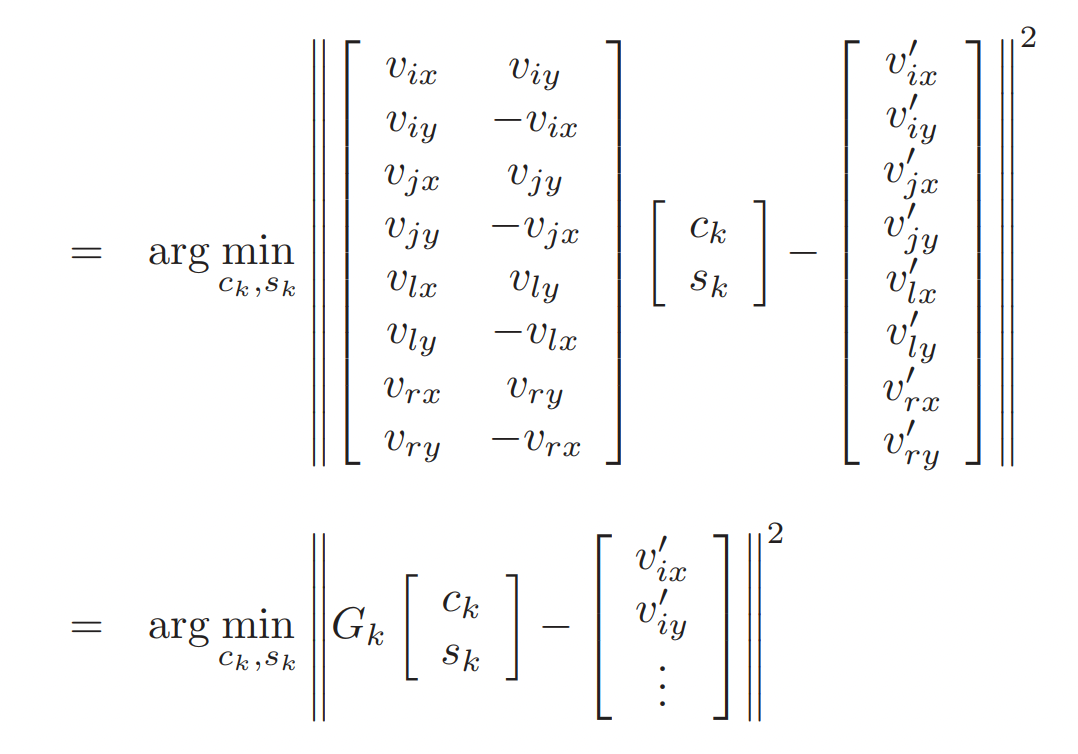
可以看出和之前一样，这也是一个形如$A x^{\prime}-b$ 的线性最小二乘优化问题。对$(c_k, v_k)^T$ 求偏导，并使其值为0，得到 \[ \left[\begin{array}{c} c_{k} \\ s_{k} \end{array}\right]=\left(G_{k}^{T} G_{k}\right)^{-1} G_{k}^{T}\left[\begin{array}{c} v_{i x}{ }^{\prime} \\ v_{i y}{ }^{\prime} \\ \vdots \end{array}\right] \] 将$T_{ij}$ 的值放到总的优化方程里如下式 \[ \arg \min _{v^{\prime} \in V}\left\{\sum_{\{i, j\} \in E}\left\|\left(v_{j}{ }^{\prime}-v_{i}^{\prime}\right)-T_{ij}\left(v_{j}-v_{i}\right)\right\|^{2}+\sum_{i \in C}\left\|\omega\left(v_{i}{ }^{\prime}-C_{i}\right)\right\|^{2}\right\} \] 其前半部分可以表示为 \[ \begin{aligned} &\left(v_{j}{ }^{\prime}-v_{i}{ }^{\prime}\right)-T_{i j}\left(v_{j}-v_{i}\right)\\ &=\left(v_{j}{ }^{\prime}-v_{i}{ }^{\prime}\right)-\left[\begin{array}{cc} c_{k} & s_{k} \\ -s_{k} & c_{k} \end{array}\right] e_{k}\\ &=\left(v_{j}{ }^{\prime}-v_{i}{ }^{\prime}\right)-\left[\begin{array}{cc} e_{k x} & e_{k y} \\ e_{k y} & -e_{k x} \end{array}\right]\left[\begin{array}{l} c_{k} \\ s_{k} \end{array}\right]\\ &=\left(v_{j}{ }^{\prime}-v_{i}{ }^{\prime}\right)-\left[\begin{array}{cc} e_{k x} & e_{k y} \\ e_{k y} & -e_{k x} \end{array}\right]\left(G_{k}^{T} G_{k}\right)^{-1} G_{k}^T\left[\begin{array}{c} v_{i x}{ }^{\prime} \\ v_{i y}{ }^{\prime} \\ \vdots \end{array}\right]\\ &=\left(\left[\begin{array}{cccccccc} -1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 1 & 0 & 0 & 0 & 0 \end{array}\right]-\left[\begin{array}{cc} e_{k x} & e_{k y} \\ e_{k y} & -e_{k x} \end{array}\right]\left(G_{k}^{T} G_{k}\right)^{-1} G_{k}^T\right) \times\left[\begin{array}{c} v_{i x}{ }^{\prime} \\ v_{i y}{ }^{\prime} \\ \vdots \end{array}\right]\\ &=\left[\begin{array}{llllllll} h_{k_{k 0}} & h_{k_{10}} & h_{k_{20}} & h_{k_{30}} & h_{k_{40}} & h_{k_{k_{0}}} & h_{k_{k_{0}}} & h_{k_{x p}} \\ h_{k_{01}} & h_{k_{11}} & h_{k_{21}} & h_{k_{31}} & h_{k_{41}} & h_{k_{k_{1}}} & h_{k_{k_{1}}} & h_{k_{71}} \end{array}\right]\left[\begin{array}{l} v_{i x}{ }^{\prime} \\ v_{i y}{ }^{\prime} \\ v_{j x}{ }^{\prime} \\ v_{j y}{ }^{\prime} \\ v_{l x}{ }^{\prime} \\ v_{l y}{ }^{\prime} \\ v_{r x}{ }^{\prime} \\ v_{r y}{ }^{\prime} \end{array}\right] \end{aligned} \] 对应的优化方程为 $\arg \min _{v^{\prime}}\left\|A_1 v^{\prime}-b_1\right\|^{2}$ , $b_1 = [0, \cdots, 0]^T$, $A_1$ = 为i,j,l,r对应位置的$h_k$ 。所以总的式子，写成矩阵的形式。表示为

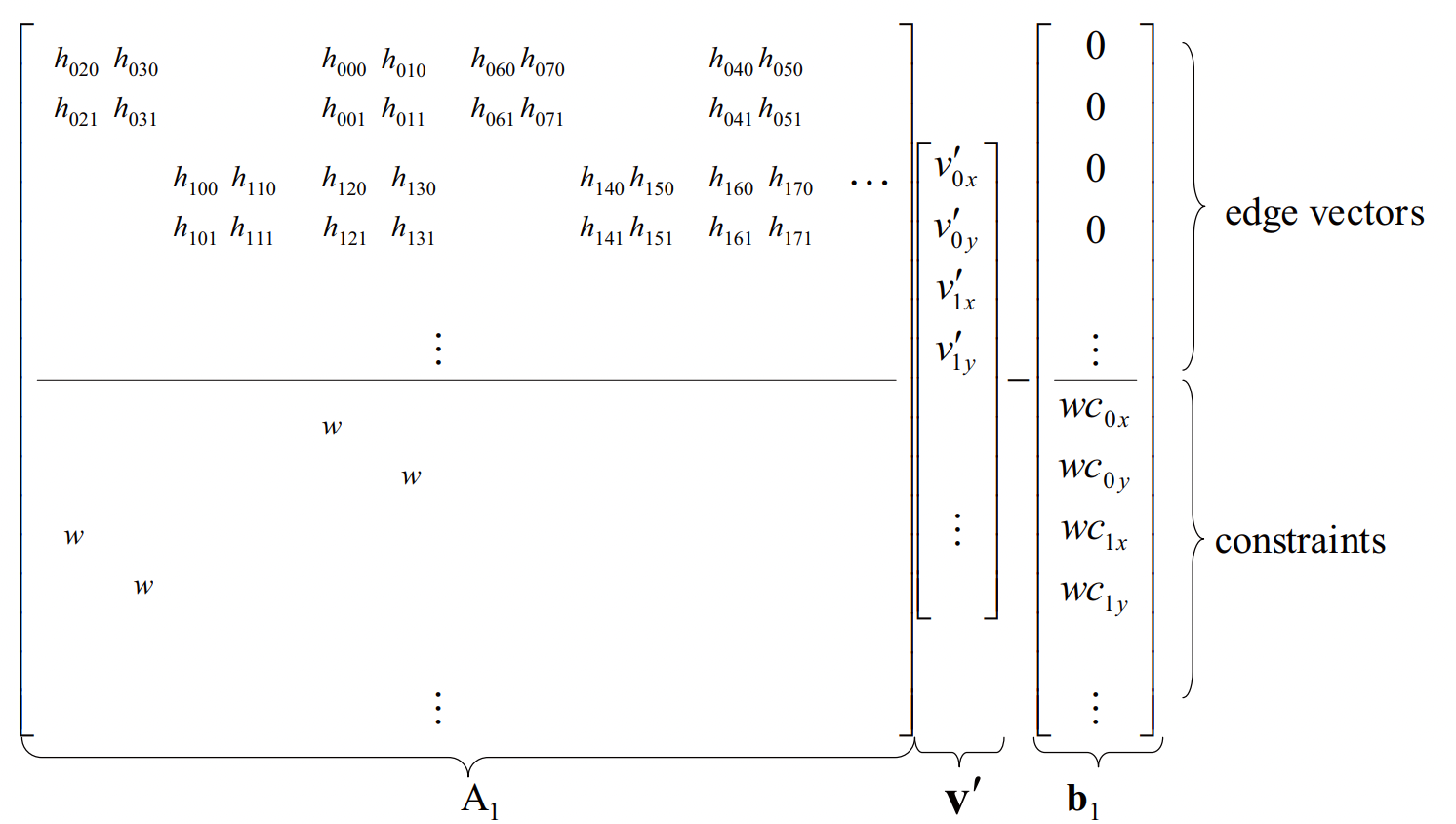
求解这个优化方程有 \[ A_1^{T} A_1 v^{\prime}=A_1^{T} b \]

Step Two - 尺度匹配

利用第一步算法的输出的旋转矩阵信息$T_k^{\prime}$为输入。并将其归一化。 \[ \left[\begin{array}{c} c_{k} \\ s_{k} \end{array}\right]=\left(G_{k}^{T} G_{k}\right)^{-1} G_{k}^{T}\left[\begin{array}{c} v_{i x}{ }^{\prime} \\ v_{i y}{ }^{\prime} \\ \vdots \end{array}\right] \]

\[ T_{k}^{\prime}=\left[\begin{array}{cc} c_{k} & s_{k} \\ -s_{k} & c_{k} \end{array}\right] \]

再对变换做一个归一化。 \[ T_{k}^{\prime}=\frac{1}{\sqrt{c_k^2+s_k^2}}\left[\begin{array}{cc} c_{k} & s_{k} \\ -s_{k} & c_{k} \end{array}\right] \] 有了$T_{ij}^{\prime}$ 后，再观察完整的优化方程有 \[ \arg \min _{v^{\prime\prime} \in V}\left\{\sum_{\{i, j\} \in E}\left\|\left(v_{j}{ }^{\prime\prime}-v_{i}^{\prime\prime}\right)-T_{ij}^{\prime}\left(v_{j}-v_{i}\right)\right\|^{2}+\sum_{i \in C}\left\|\omega\left(v_{i}{ }^{\prime\prime}-C_{i}\right)\right\|^{2}\right\} \] 此时其相对优化方程就是常量$T$。所以这个优化方程还是和之前一样的线性最小二乘优化。和之前一样可以写成下式 \[ \arg\min_{v^{\prime\prime}}||A_2 v^{\prime\prime}-b_2||^2 \] 同样按照 $x$ 和 $y$ 分开计算

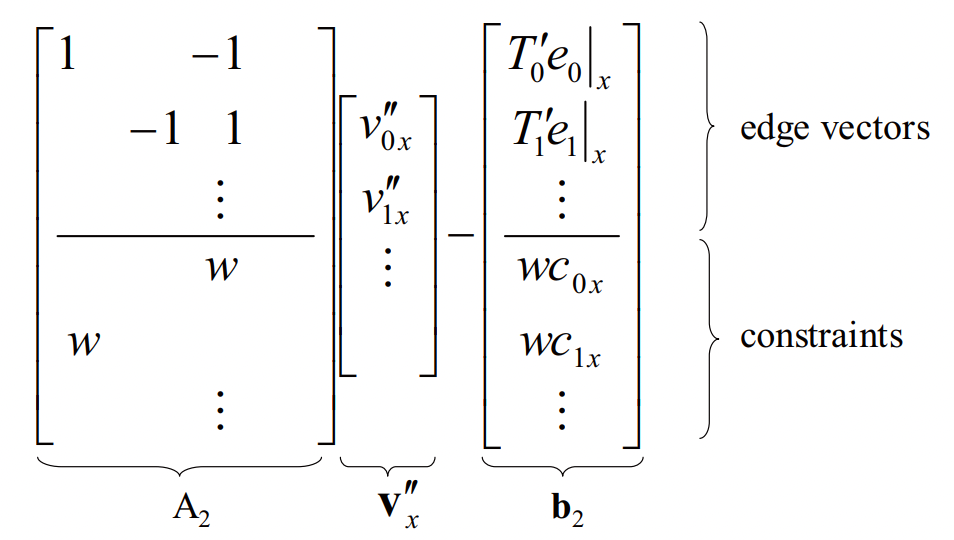
观察这个形式和第一步类似，但是$b$中的"边"向量是第一步的结果生成。总的来说，这两个两矩阵有很多矩阵可以预计算得到。 \[ A_1^{T} A_1 v^{\prime}=A_1^{T} b_1 \]

\[ A_2^{T} A_2 v^{\prime\prime}=A_2^{T} b_2 \]

$A_1$ 和 $A_2$ 的上半部分是由原始图形的点集获得。所以在一开始就可以预计算得到。

$A_1$ 和 $A_2$ 的下半部分是在点击控制点时实时计算，$\omega$ 值直接在点击控制点时赋值上去就好。

$b_1$ 和 $b_2$ 则是由控制点坐标组成在用户拖动控制点时实时变化生成。

这样通过求解这两个线性方程组，就可以得到最终的形变后点的新坐标。