强化学习是最近很火的一个研究方向,并且在多个领域取得成功,比如AlphaGo 和Dota2的AI选手,星际争霸2最近也取得了很多的突破。学习的一点心得体会记录下来。
深度强化学习基本概念
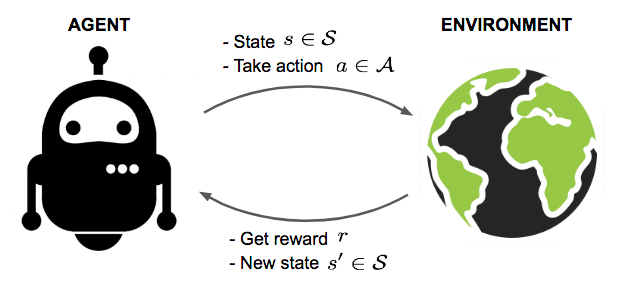
Agent 在与Environment中根据目前所处的State决定采用哪些Action,基于采取的行动,Agent收到相对应Reward,我们的目标是学习在任何特定的状态下采取行动,以最大化积累奖励。
我们把在t时刻的state, action, reward表示为\(S_t,A_t,R_t\) 所以整个交互过程可以表示为 \[ S_1,A_1,R_2,S_2,A_2,\dots,S_T \] # 马尔科夫决策过程
马尔可夫过程是描述一系列可能状态的随机模型
更正式的说,几乎所有的RL问题都可以定义为马尔科夫决策过程,这是学习RL绕不开的一个概念。
在马尔科夫决策过程中所有的状态(states)可以被认为其具有马尔可夫性质( “Markov” property)即:未来状态仅依赖于当前状态 \[ \mathbb{P}[ S_{t+1} \vert S_t ] = \mathbb{P} [S_{t+1} \vert S_1, \dots, S_t] \tag{Eq.1} \]
马尔可夫过程
马尔可夫过程是一个随机过程,也就是从当前状态\(s\)是以一定概率到\(P_{ss^{'}}\)到下个状态\(s^{'}\)。例如我们在一个马尔可夫过程中,告诉智能体向左转,但是我们智能体在环境可能会遇到某些特殊情况,导致我们只会有0.998的概率确实向左转。剩下的0.002的概率是由环境决定下一个状态。
\(P_{ss^{'}}\)可以被认为是状态转移矩阵\(P\)中的一个值,定义为从所以状态s到所有后继状态\(s^{'}\)的转移概率 \[ \mathbf{P} = from \stackrel{\mathit{to}}{\left[ \begin{array}{ccc} P_{11} & \ldots& P_{1n}\\\\ \vdots & \ddots & \vdots\\\\ P_{n1} & \ldots & P_{nn} \end{array} \right]} \] 式中n为状态数量, 矩阵中每一行的元素和为1 马尔可夫过程 又称为马尔可夫链,它是一个无记忆的随机过程,可以用元组\(<S,P>\)表示,其中\(S\)是有限数量的状态集,\(P\)是状态转移概率矩阵。
马尔可夫奖励过程
马尔可夫奖励过程也是元组,在马尔可夫过程基础上增加了奖励\(R\)和衰减系数\(\gamma\in(0,1)\) ,元组可以表示为\(<S,P,R,\gamma>\) \(R\)是奖励函数。\(S\)状态下的奖励是某一时刻\(t\)处在状态\(s\)下,在下一个时刻\(t+1\)时能获得奖励期望: \[ R_s = \mathbb{E} [R_{t+1} \vert S_t = s] \]
衰减系数\(\gamma\)的引入的原因 1. 有数学表达式的简便,避免了无限循环。 2. 现实生活中远期利益具有不确定性。引入衰减系数更加符合人们的常识。
我们感兴趣的主要是最大化积累奖励\(G_t\),他是智能体(agent)在一个马尔科夫奖励链上从t时刻开始往后所有的奖励的有衰减的总和。其中衰减系数体现了未来的奖励在当前时刻的价值比例。\(\gamma \rightarrow0\)表明趋向于“短视”性收益;\(\gamma \rightarrow 1\)则表明偏重考虑长远的收益。 \[ G_t = R_{t+1} + \gamma R_{t+2} + \dots = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} \]
价值函数Value Function
价值函数给出了某一状态或某一行为的长期价值。
价值函数\(v(s)\),定义:一个马尔科夫奖励过程中某一状态的价值函数为从该状态开始的马尔可夫链收获的期望: \[v(s) = \mathbb{E}[G_t \vert S_t = s] \]
利用价值函数定义公式可以推导出贝尔曼方程(Bellman equation)
\[ \begin{aligned} v(s) &= \mathbb{E}[G_t \vert S_t = s] \\\\ &= \mathbb{E} [R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \dots \vert S_t = s] \\\\ &= \mathbb{E} [R_{t+1} + \gamma (R_{t+2} + \gamma R_{t+3} + \dots) \vert S_t = s] \\\\ &= \mathbb{E} [R_{t+1} + \gamma G_{t+1} \vert S_t = s] \\\\ &= \mathbb{E} [R_{t+1} + \gamma v(S_{t+1}) \vert S_t = s] \end{aligned} \] 推导比较简单,只是在最后\(G_{t+1}\)变成了\(v(S_{t+1})\) 理由是收获的期望等于收获期望的期望。可以看得 价值函数可由两部分组成,一是该状态的即时奖励期望,即时奖励期望等于即时奖励,因为根据即时奖励的定义,它与下一个状态无关;另一个是下一时刻状态的价值期望,可以根据下一时刻状态的概率分布得到其期望。
Bellman 方程
马尔可夫奖励过程的Bellman方程
\[ v(s)= \mathbb{E} [R_{t+1} + \gamma v(S_{t+1}) \vert S_t = s] \] 该函数被称为马尔可夫奖励过程的Bellman方程,也可以由如下节点展示
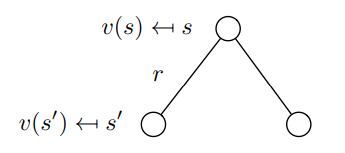
为了计算出\(s\)状态下的价值函数\(v(s)\)。需要对所有以概率\(P_{ss^{'}}\)被转移到\(s^{'}\)状态下的价值函数值求和,再加上到当前状态的即时回报\(R_s\),可以写成: \[ v(s) = R_s + \gamma \sum_{s' \in \mathcal{S}} P_{ss'} v(s') \] ### Bellman方程的矩阵形式和求解
\[ v = R +\gamma P v \]
矩阵的具体表达形式: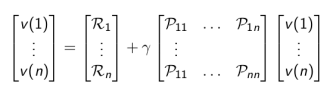
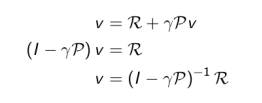
实际上,计算复杂度是 \(O(n^{3})\), n 是状态数量。因此直接求解仅适用于小规模的MRPs。大规模MRP的求解通常使用迭代法。常用的迭代方法有:动态规划Dynamic Programming、蒙特卡洛评估Monte-Carlo evaluation、时序差分学习Temporal-Difference。
马尔可夫决策过程(Markov Decision Process)
相较于马尔科夫奖励过程,马尔科夫决策过程多了一个动作集合\(A\),为当前状态下可以采取的动作,可以表示成这样的一个元组\(<S,A,P,R,\gamma>\)。此时从状态\(s\)的直接回报还依赖于在当前状态下选取的动作\(a\),表示为: \[ R(s, a) = \mathbb{E} [R_{t+1} \vert S_t = s, A_t = a] \]
策略(Policy)
此时我们将讨论主体如何决定在特定状态下必须采取哪些动作。 这由策略来\(\pi\)表示,从数学上来说策略\(\pi\)是给定状态下可采取的动作的概率分布。
对于过程中某一状态\(s\)采取可能行为\(a\)的概率分布由: * Deterministic \(\pi(s) = a\) * Stochastic \(\pi(a \vert s) = \mathbb{P}_\pi [A=a \vert S=s]\)
现在有了策略函数,我们可以得到基于策略\(\pi\)的状态价值函数为:表示从状态\(s\)开始,遵循当前策略\(\pi\)时所获得的收获的期望
\[ v_{\pi}(s) = \mathbb{E}_{\pi}[G_t \vert S_t = s] \]
动作-价值函数(Action-Value Function)
除了状态价值函数,还有一个重要的概念为动作价值函数\(q_{\pi}(s,a)\)表示在执行策略\(\pi\)时,对当前状态\(s\)执行某一具体动作\(a\)所能的到的收获的期望;或者说在遵循当前策略\(\pi\)时,衡量对当前状态执行动作\(a\)的价值大小。 \[ q_{\pi}(s, a) = \mathbb{E}_{\pi}[G_t \vert S_t = s, A_t = a] \]
和前文介绍的状态-价值函数\(V_{\pi}(s)\)类似,动作-价值函数\(q_{\pi}(s,a)\)一样可以被拆分为以下形式: \[ q_{\pi}(s, a) = \mathbb{E} [R_{t+1} + \gamma q_{\pi}(S_{t+1}, A_{t+1}) \vert S_t = s, A_t = a] \]
\(v_{\pi}(s)\)和\(q_{\pi}(s,a)\)的关系
从图中我们可以看出来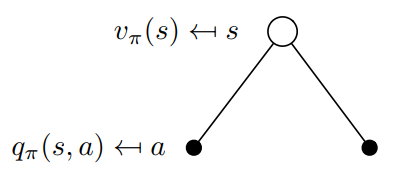
空心较大圆圈表示状态,黑色实心小圆表示的是动作本身,连接状态和动作的线条仅仅把该状态以及该状态下可以采取的行为关联起来。可以看出,在遵循策略\(\pi\)时,状态\(s\)的价值体现为在该状态下遵循某一策略而采取所有可能行为的价值按行为发生概率的乘积求和。 \[ v_{\pi}(s)= \sum_{a \in \mathcal{A}} \pi(a \vert s) q_{\pi}(s, a) \]
让我们考虑上图中的相反情况。根现在是一个我们选择采取特定动作的状态。由于马尔可夫过程是随机的。 采取行动并不意味有100%转移到下一个确定的状态。 严格来说,必须考虑在采取行动后最终进入其他状态的概率。 在采取行动后,Agent可能最终处于状态\(s^{'}\)类似的,一个行为-价值函数也可以表示成状态-价值函数的形式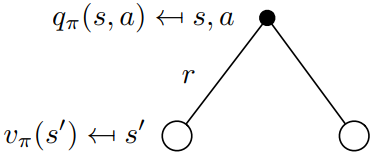
\[ q_{\pi}(s, a) = R(s, a) + \gamma \sum_{s' \in \mathcal{S}} P_{ss'}^a v_{\pi} (s') \]
从将上面两式结合起来可以得到\(q_{\pi}(s, a) \leftarrow q_{\pi} (s', a')\) 要注意到这种递推关系:
\[ q_{\pi}(s, a) = R(s, a) + \gamma \sum_{s' \in \mathcal{S}} P_{ss'}^a \sum_{a' \in \mathcal{A}} \pi(a' \vert s') q_{\pi} (s', a') \]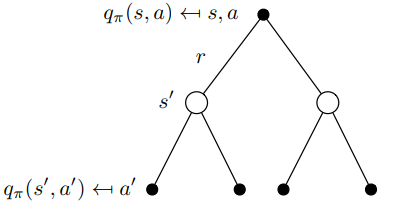
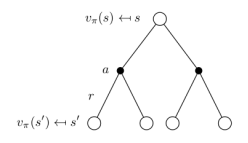
同理可得\(v_{\pi}(s) \leftarrow v_{\pi} (s')\) \[ v_{\pi}(s) = \sum_{a \in \mathcal{A}} \pi(a \vert s) \big( R(s, a) + \gamma \sum_{s' \in \mathcal{S}} P_{ss'}^a v_{\pi} (s') \big) \]
最优策略
强化学习中最重要的主题是找到最优动作 使得回报最大化。
最优状态价值函数\(v_{\*}(s)\)指的是在从所有策略产生的状态价值函数中,选取使状态\(s\)价值最大的函数: \[ v_{\*} = \max_{\pi} v_{\pi}(s) \]
类似的,最优行为价值函数\(q_{*}(s,a)\)指的是从所有策略产生的行为价值函数中,选取是状态行为对\(<s,a>\) 价值最大的函数:
\[ q_{\*}(s,a) = \max_{\pi} q_{\pi}(s,a) \]
寻找最优策略
当对于任何状态\(s\),遵循策略\(\pi\)的价值不小于遵循策略\(\pi'\)下的价值,则策略\(\pi\)优于策略\(\pi'\): \[ \pi \geq \pi' \quad if v_{\pi}(s)\geq v_{\pi'}(s), \forall s \] 定理 对于任何MDP,下面几点成立: 1. 存在一个最优策略,比任何其他策略更好或至少相等; 2. 所有的最优策略有相同的最优价值函数; 3. 所有的最优策略具有相同的行为价值函数。
可以通过最大化最优行为价值函数来找到最优策略:
对于任何MDP问题,总存在一个确定性的最优策略;同时如果我们知道最优行为价值函数,则表明我们找到了最优策略。 \[ \pi_{\*}(a|s) = \begin{cases} 1 & if \quad a =\mathop{\arg\max}\limits_{a\in\mathcal{A}} q_{\*}(s,a) \\\\ 0 & otherwise \end{cases} \]
贝尔曼最优方程(Bellman Optimality Equation)
针对\(v_{\*}\),一个状态的最优价值等于从该状态出发采取的所有行为产生的行为价值中最大的那个行为价值: \[ v_{\*}(s) = \max_{a \in \mathcal{A}} q_*(s,a) \]
对于 \(q_{\*}\),在某个状态\(s\)下,采取某个行为的最优价值由2部分组成,一部分是离开状态 \(s\)的即刻奖励,另一部分则是所有能到达的状态\(s'\) 的最优状态价值按出现概率相乘求和: \[ q_{\*}(s, a) = R(s, a) + \gamma \sum_{s' \in \mathcal{S}} P_{ss'}^a v_{\*}(s') \]
将以上两式组合起来有: \[ v_{\*}(s) = \max_{a \in \mathcal{A}} \big( R(s, a) + \gamma \sum_{s' \in \mathcal{S}} P_{ss'}^a v_{\*}(s') \big) \]
\[ q_{\*}(s, a) = R(s, a) + \gamma \sum_{s' \in \mathcal{S}} P_{ss'}^a \max_{a' \in \mathcal{A}} q_{\*}(s', a') \]
以上就是贝尔曼最优方程 和之前的贝尔曼期望方程结构非常相似。
如果我们拥有环境的全部信息,这样问题变成一个规划问题,可以用动态规划求解。但是在大多数情景下,我们并不知道\(P_{ss'}^a\),\(R(s,a)\)。所以我们不能直应用贝尔曼方程对MDP进行求解。但是贝尔曼方程是很多强化学习算法的理论基础。务必掌握。